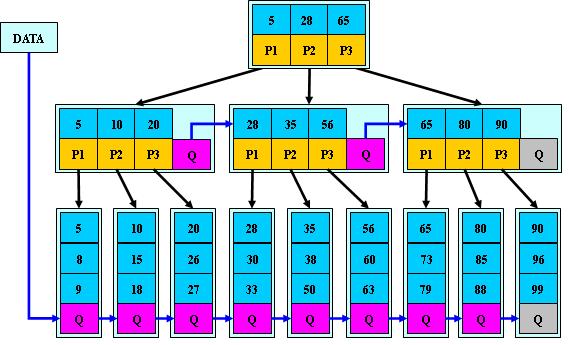
B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。

　　所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。(而B 树的叶子节点并没有包括全部需要查找的信息)

　　所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。(而B 树的非终节点也包含需要查找的有效信息)

　　1) 有n棵子树的结点中含有n个关键字； (B~树是n棵子树有n+1个关键字) 2) 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (B~树的叶子节点并没有包括全部需要查找的信息) 3) 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (B~树的非终节点也包含需要查找的有效信息) B+树的有效内容均在叶子节点，B-树的有效内容不全在叶子节点上 B+树的头指针有两个，一个指向根节点，另一个指向关键字最小的元素，因此B+树有两种遍历的方式： 1.从根节点开始随机查询 2.从最小关键词顺序查询

　　B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。

　　举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B+树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

　　由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

　　1.定义任意非叶子结点最多只有M个儿子；且M2； 2.根结点的儿子数为[2, M]； 3.除根结点以外的非叶子结点的儿子数为[M/2, M]； 4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字） 5.非叶子结点的关键字个数=指向儿子的指针个数-1； 6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] K[i+1]； 7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树； 8.所有叶子结点位于同一层；

　　1、红黑树放弃了追求完全平衡，追求大致平衡，在与平衡二叉树的时间复杂度相差不大的情况下，保证每次插入最多只需要三次旋转就能达到平衡，实现起来也更为简单。

　　2、平衡二叉树追求绝对平衡，条件比较苛刻，实现起来比较麻烦，每次插入新节点之后需要旋转的次数不能预知。

　　B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

　　学习自平衡二叉树 B树（图中示例为m=3阶）每个节点（除了根节点）有：2lt;=klt;=m个子节点关键...博文来自：的博客