插入和删除操作改变树的平衡性的概率要远远小于AVL（RBT不是高度平衡的）。因此需要的旋转操作的可能性要小，而且一旦需要旋转，插入一个结点最多只需要旋转2次，删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在O(logN)，但是实际上，这种操作由于简单所需要的代价很小。

　　红黑树能够以O(log2(N))的时间复杂度进行搜索、插入、删除操作。此外,任何不平衡都会在3次旋转之内解决。这一点是AVL所不具备的。

　　插入操作： 1.插入根节点（不需要操作） 2.父节点为黑色(不需要操作) 3.父节点和兄弟节点为红色，祖父节点为黑色，只需要变色，将祖父节点递归检查（原本检查自己） 4.父节点为红色，兄弟节点为黑色，祖父节点为红色，先两次旋转再调整颜色（左旋+右旋）

　　删除操作： 1.删除只有一个新的根节点（直接删除） 2.父节点为黑色，兄弟节点为红色（先旋转成左左，再删除） 3.父节点为黑色，兄弟节点为黑色（先将兄弟节点换成红色，变成情况2） 4.父节点为红色，自己和兄弟节点为黑色（将父节点变成黑色，兄弟节点变成红色，变成情况2） 5.兄弟节点为黑色，兄弟节点左子树根节点为红色（交换颜色，旋转成为左左） 6.情况2和情况5，调整性质5（将N删掉，用子节点顶替，若子节点为红色，则重绘为黑色）

　　3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：m/2= k = m ；

　　4) 所有叶子结点都出现在同一层，叶子结点不包含任何关键字信息(可以看做是外部接点或查询失败的接点，实际上这些结点不存在，指向这些结点的指针都为null)；

　　5) 每个非终端结点中包含有n个关键字信息： (n，A0，K1，A1，K2，A2，……，Kn，An)。其中，

　　b) Ai为指向子树根的接点，且指针A(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。

　　由于B~树结点中的关键字个数必须=[m/2]-1。因此和平衡二叉树不同，每一次插入一个关键字并不是在树中添加一个结点，而是首先在最低层的某个非终端结点中添加一个关键字，若该结点的关键字个数不超过m-1，则插入完成。否则，要产生结点的”分裂” 。

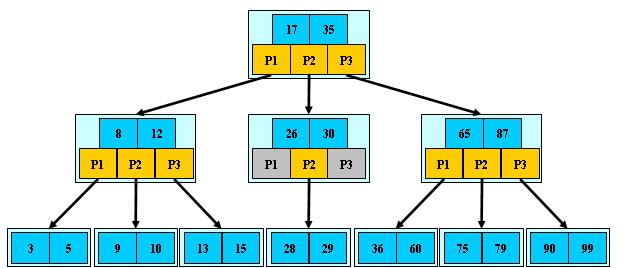
　　我们现在把整棵树构造在磁盘中，假如每个盘块可以正好存放一个B~树的结点（正好存放2个文件名）。那么一个BTNode结点就代表一个盘块，而子树指针就是存放另外一个盘块 （详细见《外部存储器—磁盘 》）的******。

　　(1) 根据根结点指针找到文件目录的根磁盘块1，将其中的信息导入内存。【磁盘IO操作1次】

　　(2) 此时内存中有两个文件名17，35和三个存储其他磁盘页面******的数据。根据算法我们发现172935，因此我们找到指针p2。

　　(3) 根据p2指针，我们定位到磁盘块3，并将其中的信息导入内存。【磁盘IO操作2次】

　　(4) 此时内存中有两个文件名26，30和三个存储其他磁盘页面******的数据。根据算法我们发现262930，因此我们找到指针p2。

　　(5) 根据p2指针，我们定位到磁盘块8，并将其中的信息导入内存。【磁盘IO操作3次】

　　(6) 此时内存中有两个文件名28，29。根据算法我们查找到文件29，并定位了该文件内存的磁盘******。

　　分析一下上面的过程，我们发现需要3次磁盘IO操作和3次内存查找操作。关于内存中的文件名查找，由于是一个有序表结构，可以利用折半查找提高效率。至于3次磁盘IO操作时影响整个B~树查找效率的决定因素。 当然，如果我们使用平衡二叉树的磁盘存储结构来进行查找，磁盘IO操作最少4次，最多5次。而且文件越多，B~树比平衡二叉树所用的磁盘IO操作次数将越少，效率也越高。

　　B+ 树是一种树数据结构，是一个n叉树，每个节点通常有多个孩子，一颗B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点，也可能是一个包含两个或两个以上孩子节点的节点。