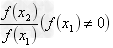9. 初值定理 如果信号 x ( t ) 的拉氏变换为 X ( s ) ， x ( t ) 在 t = 0 点不含有任何阶 且 次的冲激函数 ，则: (5.40) 初值定理表明，s X ( s ) 的极限值等于信号 x ( t ) 在 t = 0 点的初值，而 且，无论拉氏变换采用 0 系统还是 0 系统，所求得的初值都是在 t = 0 时刻的 值，证明如下。 根据时域微分性质可知: + + + (5.41) 而由拉氏变换的定义可得: (5.42) 于是有: (5.43) 对此式两边取 因此: 的极限，由于当，且仅当 t 0 时， ， 对初值定理，也可利用信号 x ( t ) 在 t = 0 时刻的台劳级数来证明，其台劳 级数为: + ( 5.44) 式中，x (n)( 0 ) 是 x ( t ) 在 t = 0 时刻的 n 阶导数值。 由于: + + 因此，对式（5.44）两边取拉氏变换后有: 由此而得: 初值定理要求信号 x ( t ) 在 t = 0 点不含有任何阶次的冲激函数 ， 这也就是要求式（5.40）中的 X ( s ) 必须是一个真分式。如果 X ( s ) 是一个 假分式，即当 X ( s ) 分子的阶次高于或等于分母的阶次时， ， 式（5.40）将不成立。因此，如果 X ( s ) 是一个假分式时，则应先将它分解出 一个线）求这个真分式所对应的信号初值。例如，如 果 ，这是一个假分式，它不能直接利用式（5.40）求得初值。 但是，如果将其分解为 信号初值为 1。 ，则可利用式（5.40）求得 所对应的 (5.40) 10.终值定理 终值定理的形式类似于初值定理，它是通过变换式在 时的极限值来求得信号的终值，即 (5.45) 利用初值定理证明过程中所得到的式（5.43）可以证明 终值定理。 由式（5.43）知 于是有: 显然只有当信号 x ( t ) 的终值存在时，才能利用式 （5.45）求得它的终值，否则将得到错误的结果。而要使 x ( t ) 的终值存在， 则要求 X ( s ) 的极点在左半 s 平面， 如 果 X ( s ) 在 j? 上有极点的话，也只能是在原点上的一阶 极点，其原因在于，只有满足这种极点分布的信号才有终值 存在。关于这个问题，可参阅“拉普拉斯逆变换”一节中的 讨论。 至此，我们讨论了单边拉氏变换的主要性质，并求得了 一些常见信号的变换式。 表 5.1 和 表 5.2 分别列出了这些信号的变换式和拉氏变换 的主要性质，以供读者查阅。 虽然我们讨论的只是单边拉氏变换，但对双边拉氏变换 而言，除了初值定理、终值定理和微分性质和单边拉氏变换 略有不同外，其它的性质和单边拉氏变换是一样的。这两种 变换之间并没有什么本质的区别，然而，如果要求解非零状 态下的系统响应，则只能使用单边拉氏变换。 4.5.8 终值定理 若 是因果序列，且已知其 z 变换为 则 证明：因为 (线性性) (时移性) 取极限可得 ＝ = [证毕] 由证明过程可以看出，终值定理只有在 位圆内(如果位于单位圆上，则只能位于 存在时才可以应用,也就是说 点，且是一阶极点)。 的极点必须在单 下面我们举例来说明终值定理的应用条件。 例：设序列为 ，可求出其 Z 变换为 ，取极限可得 。但显然序列的极限并不存在，即 不存在，所以 导致上面这种“终值定理”不成立的原因是 X(z)(还是 X(z)(z-1)？)在单位圆外有极点。 终值定理的应用类似于拉氏变换的终值定理，如果已知序列 x(n)的 z 变换 X(z)，在不求逆变换，且满 足终值定理地应用条件时，就可以直接利用终值定理很方便地求出序列的终值