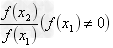声明：百科词条人人可编辑，词条创建和修改均免费，绝不存在官方及代理商付费代编，请勿上当受骗。详情

　　T检验，亦称student t检验（Students t test），主要用于样本含量较小（例如n 30），总体标准差σ未知的正态分布。

　　单总体t检验是检验一个样本平均数与一个已知的总体平均数的差异是否显著。当总体分布是正态分布，如总体标准差未知且样本容量小于30，那么样本平均数与总体平均数的呈t分布。

　　是检验两个样本平均数与其各自所代表的总体的差异是否显著。双总体t检验又分为两种情况，一是独立样本t检验（各实验处理组之间毫无相关存在，即为独立样本），该检验用于检验两组非相关样本被试所获得的数据的差异性；一是配对样本t检验，用于检验匹配而成的两组被试获得的数据或同组被试在不同条件下所获得的数据的差异性，这两种情况组成的样本即为相关样本。

　　检验的扩展，不过检验的对象由一群来自常态分配独立样本更改为二群配对样本之观测值之差。若二配对样本

　　：μ ≠ μ0（备择假设alternative hypothesis）

　　, P 0.05，按α=0.05水准，不拒绝H0，两者的差别无统计学意义。

　　1、选用的检验方法必须符合其适用条件(注意：t检验的前提：1.来自正态分布总体； 2.随机样本 ；3.均数比较时，要求两样本总体方差相等，即具有方差齐性)

　　2、区分单侧检验和双侧检验。单侧检验的界值小于双侧检验的界值，因此更容易拒绝，犯第Ⅰ错误的可能性大

　　，越有理由说明两者有差异，差别有无统计学意义和有无专业上的实际意义并不完全相同。

　　5、假设检验和可信区间的关系结论具有一致性差异：提供的信息不同区间估计给出总体均值可能取值范围，但不给出确切的概率值，假设检验可以给出H

　　检验之运算，诸如QtiPlot、Calc、LibreOffice Calc、Microsoft Excel、SAS、SPSS、Stata、DAP、gretl、R、Python、PSPP、Minitab等

　　：其零假设为两个正态分布的总体的均值是相同的。这一检验通常被称为学生t检验。但更为严格地说，只有两个总体的方差是相等的情况下，才称为学生t检验；否则，有时被称为Welch检验。以上谈到的检验一般被称作“未配对”或“独立样本”t检验，我们特别是在两个被检验的样本没有重叠部分时用到这种检验方式

　　。举例来说，我们测量一位病人接受治疗前和治疗后的肿瘤尺寸大小。如果治疗是有效的，我们可以推定多数病人接受治疗后，肿瘤尺寸变小了。这种检验一般被称作“配对”或者“重复测量”t检验。

　　为了进行独立样本t检验，需要一个自（分组）变量（如性别：男、女）与一个因变量（如身高测量值）。根据自变量的特定值，比较各组中因变量的均值。用t检验比较下列男、女儿童身高的均值

　　3、选择SPSS中compare means菜单， 独立样本， t-test。选择双侧检验，以及统计显著性水平α=0.05 运行

　　Fisher Box, Joan. Guinness, Gosset, Fisher, and Small Samples. Statistical Science. 1987, 2 (1): 45–52.

　　OConnor, John J.; Robertson, Edmund F., Gosset, MacTutor History of Mathematics archive