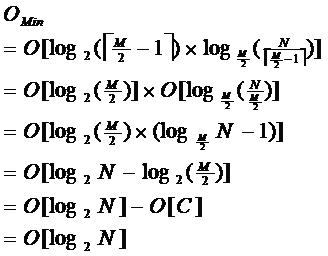，B即Balanced，平衡的意思。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是另一种树。而事实上是，

　　3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

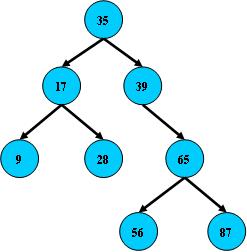
　　二叉搜索树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；

　　否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入

　　如果二叉搜索树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树

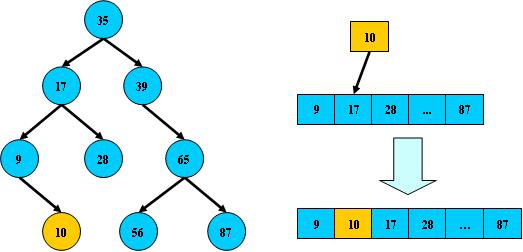
　　的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变二叉搜索树结构

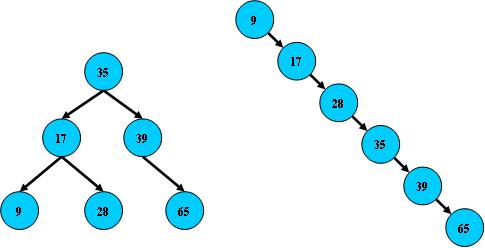
　　右边也是一个二叉搜索树，但它的搜索性能已经是线性的了；同样的关键字集合有可能导致不同的

　　树结构索引；所以，使用二叉搜索树还要考虑尽可能让B树保持左图的结构，和避免右图的结构，也就

　　实际使用的二叉搜索树都是在原二叉搜索树的基础上加上平衡算法，即“平衡二叉树”；如何保持B树

　　结点分布均匀的平衡算法是平衡二叉树的关键；平衡算法是一种在二叉搜索树中插入和删除结点的

　　4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

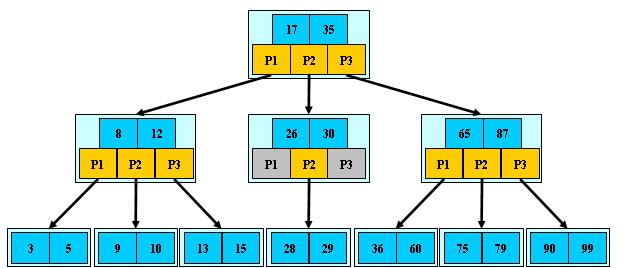
　　B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果

　　命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为

　　由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少

　　所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

　　3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树

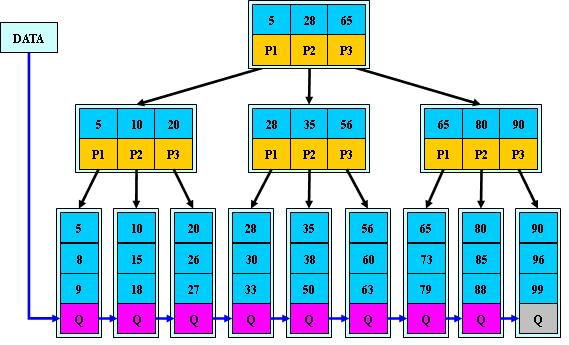
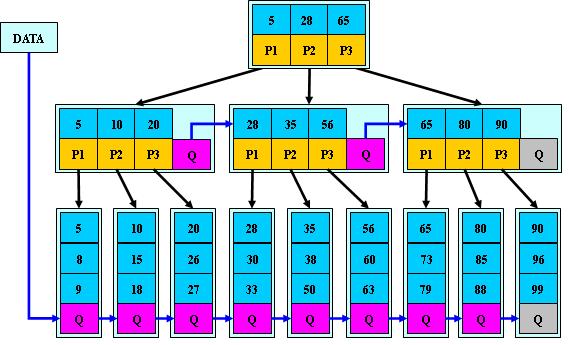
　　B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在

　　1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好

　　B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3

　　B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据

　　复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父

　　数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字

　　（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之

　　间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

　　二叉搜索树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于

　　B（B-）树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键

　　背景:这几天在看《高性能Mysql》,在看到创建高性能的索引,书上说mysql的存储引擎InnoDB采用的索引类型是B+Tree,那么,大家有没有产生这样一个疑问,对于数据索引,为什么要使用B+Tre...博文来自：杨龙飞的博客